什么是动态规划
- 分治方法将问题划分为互不相交的子问题,递归的求解子问题,再将它们的解组合起来,求出原问题的解。
- 动态规划将复杂的问题分解为若干子问题,通过综合子问题的最优解来得到原问题的最优解,并将每个求解过的子问题记录下来,这样下次碰到相同的子问题,就可以直接使用之前记录的结果,而不重复计算。
动态规划适用情况与场景
- 适用情况: 一个问题必须拥有重叠子问题和最优子结构,才能使用动态规划去解决
- 适用场景: 最大值/最小值, 可不可行, 是不是,方案个数
动态规划解题步骤
- 定义子问题
- 写出子问题的递推关系
- 确定 DP 数组的计算顺序
- 空间优化(可选)
步骤一、定义子问题
子问题是和原问题相似,但规模较小的问题。
例:
原问题「从全部房子中能偷到的最大金额」→ 子问题「从k个房子中能偷到的最大金额」子问题需要具备以下两个性质:
- 原问题要能由子问题表示
- 一个子问题的解要能通过其他子问题的解求出
步骤二、写出子问题的递推关系
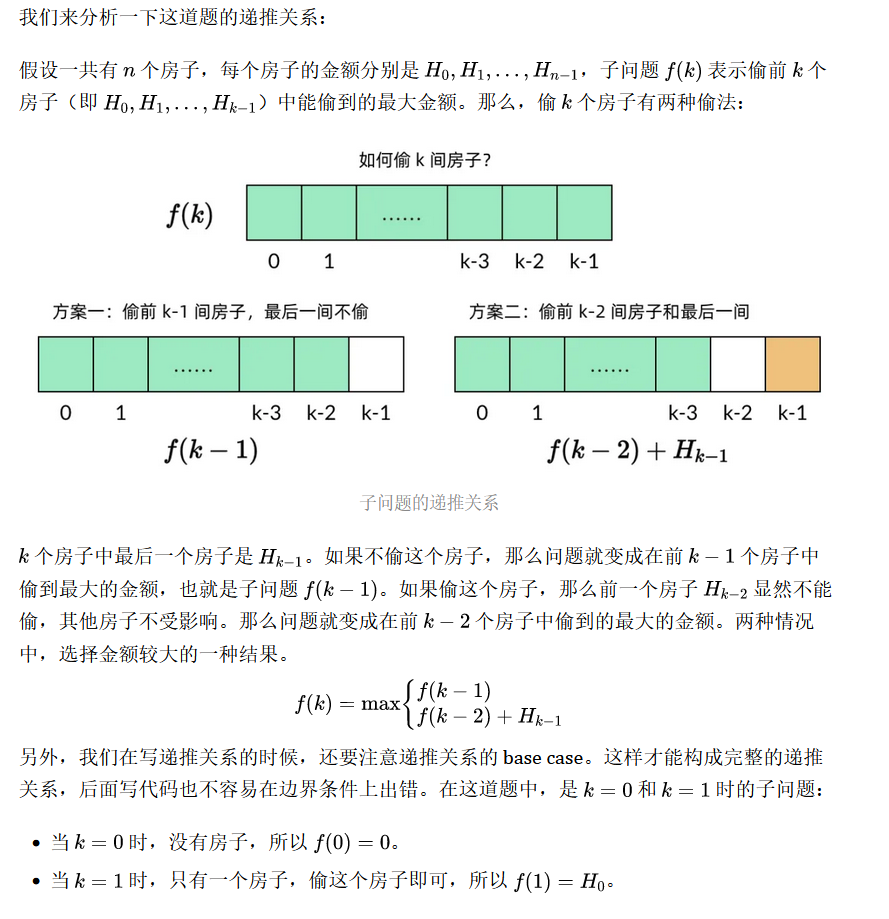
步骤三、确定 DP 数组的计算顺序
动态规划有两种计算顺序:
- 一种是自顶向下的、使用备忘录的递归方法
- 一种是自底向上的、使用 DP 数组的循环方法
不过在普通的动态规划题目中,99% 的情况我们用循环方法就很好解决,所以我们最好在一开始就坚持自底向上方法,使用 DP 数组,这样才有助于领悟动态规划的真正精髓。
步骤四、空间优化
空间优化的基本原理是,很多时候我们并不需要始终持有全部的 DP 数组。
